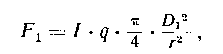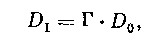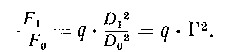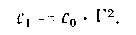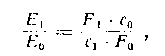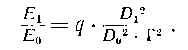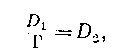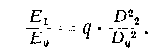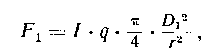той его части, которая теряется в самом приборе вследствие поглощения в стекле п отражения от поверхностей линз. Обозначив через q коэффициент прозрачности прибора, находим, что световой поток, прошедший через прибор и попадающий в глаз, будет равен

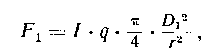(9.2)

где £>j — диаметр входного зрачка. Так как при нормальном увеличении

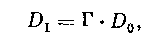(9.3)

то отношение световых потоков и видимых яркостей будет равно

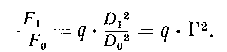(9.4)

При увеличении, большем нормального, в глаз попрежнему попадает весь световой поток, прошгдший через прибор. При увеличении, меньшем нормального, выходным зрачком является зрачок глаза, а входным — изображение зрачка глаза через окуляр и объектив (в обратном ходе лучей). Отношение диаметров входного и выходного зрачков при этом не изменяется. Таким образом равенство (9,4) остается в силе для всех случаев наблюдения точечных объектов через телескопическую систему; видимая яркость точечных объектов пропорциональна квадрату увеличения прибора.

Иной результат получается при наблюдении широких светящихся освещенных предметов. Изображение таких предметов на сетчатке захватывает несколько светочувствительных элементов. В этом случае видимая, или субъективная, яркость определяется освещенностью на сетчатке и, следовательно, зависит также от размеров изображения на сетчатке глаза.

При наблюдении невооруженным глазом световой поток распределяется на некоторой площади сетчатки с₀. Освещенность Е₀ на сетчатке и видимая яркость р

пропорциональны — При наблюдении того же объекта в зрительную трубу

^со

световой поток, определяемый равенством (9,1), распределяется на площади сетчатки c_v определяемой из равенства

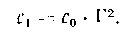(9.5)

Освещенность на сетчатке Е_L и видимая яркость теперь пропорциональны

р

—¹. Отношение видимых яркостей при наблюдении через прибор и для невоору-женного глаза будет

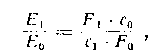(9.6)

или, в силу равенств (9,4) и (9,5),

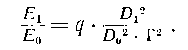(9.7)

На основании (5,6) можно написать соотношение

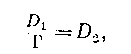(9.8)

где D._z — диаметр выходного зрачка; равенство (9,7) может быть представлено в виде